Neural-network quantum states for a two-leg Bose-Hubbard ladder under magnetic flux
Abstract
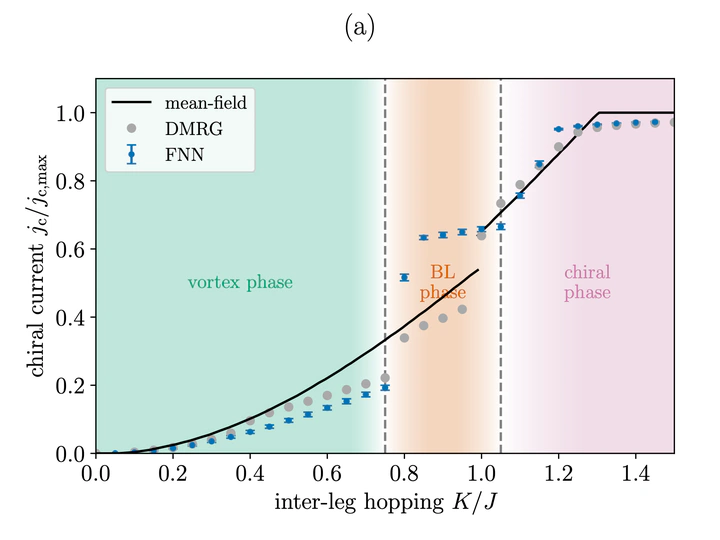
Quantum gas systems are ideal analog quantum simulation platforms for tackling some of the most challenging problems in strongly correlated quantum matter. However, they also expose the urgent need for new theoretical frameworks. Simple models in one dimension, well studied with conventional methods, have received considerable recent attention as test cases for new approaches. Ladder models provide the logical next step, where established numerical methods are still reliable, but complications of higher dimensional effects like gauge fields can be introduced. In this paper, we investigate the application of the recently developed neural-network quantum states in the two-leg Bose-Hubbard ladder under strong synthetic magnetic fields. Based on the restricted Boltzmann machine and feedforward neural network, we show that variational neural networks can reliably predict the superfluid-Mott insulator phase diagram in the strong coupling limit comparable with the accuracy of the density-matrix renormalization group. In the weak coupling limit, neural networks also diagnose other many-body phenomena such as the vortex, chiral, and biased-ladder phases. Our work demonstrates that the two-leg Bose-Hubbard model with magnetic flux is an ideal test ground for future developments of neural-network quantum states.